Rangkuman Materi Gerak Harmonik Sederhana
Pada kesempatan kali ini kita akan mempelajari tentang gerak harmonik sederhana. apa yang kita pelajari dalam materi kali ini? ada beberapa besaran yang harus dipahami pada materi ini.salah satunya yaitu getaran dan gelombang, Persamaan umum gelombang dan masih banyak lagi. untuk lebih jelasnya kita langsung saja yuukk simak.!
Pengertian Getaran
Getaran merupakan gerakan bolak-balik secara periodik melalui titik kesetimbangan.
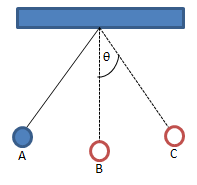
Getaran pada ayunan sederhana
A dan C disebut titik tertinggi sedangkan B disebut titik kesetimbangan. Satu getaran terjadi saat bandul melintas mulai dari A dan kembali lagi ke A. Jadi satu getaran itu dari A – B – C – B – A.
Satu getaran lengkap adalah gerakan bolak-balik dari A ke C dan kembali lagi ke A. Waktu yang dibutuhkan untuk melakukan satu getaran lengkap disebut periode. Sedangkan banyaknya getaran atau gerak bolak-balik yang dapat dilakukan dalam waktu satu detik disebut frekuensi. Hubungan periode (T) dan frekuensi (f) dinyatakan oleh:
Gaya pemulih, periode dan frekuensi ayunan sederhana
Gaya pemulih merupakan gaya yang menyebabkan benda kembali ke keadaan semula. Dirumuskan sebagai berikut:
F = – k.x atau
F = -m.g.sin θ atau
Keterangan:
F : gaya (N)
k : tetapan gaya
m : massa benda (kg)
g : percepatan gravitasi (m/s2)
θ : sudut simpangan
l : panjang tali (m)
x : simpangan getar (m)
Tanda minus (-) menunjukkan bahwa arah gaya F berlawanan dengan arah simpangan.
Periode getaran pada ayunan sederhana
Dirumuskan sebagai berikut:
Frekuensi getaran pada ayunan sederhana
Dirumuskan sebagai berikut:
T : periode getaran (s)
g : percepatan gravitasi (ms-2)
π : 3.14 = 22/7
l : panjang tali (m)
f : frekuensi getaran (Hz)
Getaran pada pegas
Gaya pemulih, periode dan frekuensi pada pegas
Gaya pemulih pada pegas dirumuskan sebagai berikut:
F = – k.∆x
Keterangan:
F : gaya yang bekerja pada pegas (N)
k : konstanta pegas (N/m)
∆x : pertambahan panjang pegas (m)
Periode Getaran Pada Pegas
Dirumuskan sebagai berikut:
Frekuensi getaran pada ayunan sederhana
Dirumuskan sebagai berikut:
T = periode getaran (s)
π = 3.14 = 22/7
k = tetapan pegas (Nm-1)
f = frekuensi getaran (Hz)
m = massa beban (kg)
Nilai konstanta suatu pegas dapat ditentukan dari persamaan:
k = m.ω2
Keterangan
ω : kecepatan sudut dari gerak pegas (rad/s)
Jika disusun seri maka menentukan k dengan persamaan:
Jika disusun paralel maka menentukan k dengan persamaan:
kparalel = k1 + k2 + k3 + ………..
Persamaan Simpangan, Kecepatan, dan Percepatan
Jika benda melakukan gerak harmonik sederhana dengan sudut awal θo maka persamaan simpangannya
y = A sin(ωt + θ0)
Keterangan:
y = Simpangan (meter)
A = Amplitudo (meter)
θ0 = Frekuensi (rad/s)
ω = Sudut fase awal (rad)
t = waktu titik tersebut telah bergetar (s)
Persamaan kecepatan getaran harmonik adalah:
v = Aωcos(ῴt + θ0)
persamaan dari percepatan gerak harmonik dinyatakan sebagai:
a = -Aω2 sin(ωt + θ0)
Sudut Fase, Fase, dan Beda Fase
Sudut fase dapat dituliskan sebagai berikut:
θ =(ῴt + θ0)
Keterangan:
Ҩ = fase.
Beda fase yang dihasilkan diantara dua kedudukan adalah
ΔҨ = Ҩ2 – Ҩ1
hukum kekekalan energi mekanik pada getaran harmonik
Semua benda yang bergerak mempunyai energi kinetik dan energi potensial. Benda yang bergerak harmonik sederhana juga mempunyai energi kinetik dan energi potensial.
Energi potensial
di rumuskan sebagai berikut
EP = ½ ky2
EP = ½ mω2 A2 sin2ωt
Keterangan
Ep = energi potensial (joule)
m = massa benda (kg)
A = amplitudo (m)
ω = kecepatan sudut(rad/s)
t = waktu (sekon)
Energi kinetik
di rumuskan sebagai berikut
Ek = ½ mv2
Ek = ½ mω2A2cos2ωt
Ek = ½ k (A2-y2)
Energi mekanik
Energi mekanik merupakan jumlah energi potensial dan energi kinetik.
EM = Ep + Ek = ½kA2.
superposisi getaran
Benda dapat mengalami dua getaran sekaligus. Jika suatu benda melakukan dua getaran sekaligus akan membentuk gelombang getaran yang di peroleh dengan menjumlahkan simpangan tiap-tiap getaran.
Elastisitas
merupakan kemampuan suatu benda untuk kembali ke keadaan semula setelah gaya yang dikenakan padanya dilepaskan. Sifat elastis suatu bahan berkaitan erat dengan modulus elastis. Modulus elastis disebut juga modulus Young.
Modulus elastis adalah perbandingan antara tegangan dan regangan yang dialami oleh suatu benda.
Tegangan merupakan hasil bagi antara gaya tarik yang dialami benda dengan luas penampangnya, dan dirumuskan:
Keterangan:
s : tegangan (N/m2)
F : gaya (N)
A : luas penampang (m2)
Regangan merupakan hasil bagi antara pertambahan panjang dengan panjang awal, dan dirumuskan:
Keterangan:
e : regangan (tanpa satuan)
∆l : pertambahan panjang (m)
lo : panjang awal (m)
l : panjang akhir (m)
Modulus elastis adalah perbandingan antara tegangan dan regangan yang dialami oleh suatu benda, dan dirumuskan:
Contoh soal dan Pembahasan Gerak Harmonik Sederhana
Soal No. 1Sebuah benda bergetar hingga membentuk suatu gerak harmonis dengan persamaan
y = 0,04 sin 20π t
dengan y adalah simpangan dalam satuan meter, t adalah waktu dalam satuan sekon. Tentukan beberapa besaran dari persamaan getaran harmonis tersebut:
a) amplitudo
b) frekuensi
c) periode
d) simpangan maksimum
e) simpangan saat t = 1/60 sekon
f) simpangan saat sudut fasenya 45°
g) sudut fase saat simpangannya 0,02 meter
Pembahasan
Pola persamaan simpangan gerak harmonik diatas adalah
y = A sin ωt
ω = 2π f
a) amplitudo atau A
y = 0,04 sin 20π t
↓
A = 0,04 meter
b) frekuensi atau f
y = 0,04 sin 20π t
↓
ω = 20π
2πf = 20π
f = 10 Hz
c) periode atau T
T = 1/f
T = 1/10 = 0,1 s
d) simpangan maksimum atau ymaks
y = A sin ωt
y = ymaks sin ωt
y = 0,04 sin 20π t
↓
y = ymaks sin ωt
ymaks = 0,04 m
(Simpangan maksimum tidak lain adalah amplitudo)
e) simpangan saat t = 1/60 sekon
y = 0,04 sin 20π t
y = 0,04 sin 20π (1/60)
y = 0,04 sin 1/3 π
y = 0,04 sin 60° = 0,04 × 1/2√3 = 0,02 √3 m
f) simpangan saat sudut fasenya 45°
y = A sin ωt
y = A sin θ
dimana θ adalah sudut fase, θ = ωt
y = 0,04 sin θ
y = 0,04 sin 45° = 0,04 (0,5√2) = 0,02√2 m
g) sudut fase saat simpangannya 0,02 meter
y = 0,04 sin 20π t
y = 0,04 sin θ
0,02 = 0,04 sin θ
sin θ = 1/2
θ = 30°
Soal No. 2
Diberikan sebuah persamaan simpangan gerak harmonik
y = 0,04 sin 100 t
Tentukan:
a) persamaan kecepatan
b) kecepatan maksimum
c) persamaan percepatan
Pembahasan
a) persamaan kecepatan
Berikut berurutan rumus simpangan, kecepatan dan percepatan:
y = A sin ωt
ν = ωA cos ω t
a = − ω2 A sin ω t
Ket:
y = simpangan (m)
ν = kecepatan (m/s)
a = percepatan (m/s2)
Dari y = 0,04 sin 100 t
ω = 100 rad/s
A = 0,04 m
sehingga:
ν = ωA cos ω t
ν = (100)(0,04) cos 100 t
ν = 4 cos 100 t
b) kecepatan maksimum
ν = ωA cos ω t
ν = νmaks cos ω t
νmaks = ω A
ν = 4 cos 100 t
↓
νmaks = 4 m/s
c) persamaan percepatan
a = − ω2 A sin ω t
a = − (100)2 (0,04) sin 100 t
a = − 400 sin 100 t
NEXT PAGE : 1 2 3