Perbandingan Trigonometri Pada Segitiga
Sisi AB merupakan sisi miring segitiga
Sisi BC merupakan sisi depan sudut
Sisi AC merupakan sisi samping sudut
Di sini kita akan mengenal istilah matematika baru, yaitu sinus (sin), cosinus (cos), tangent (tan), cosecan (csc), secan (sec) dan cotangent (cot), yang mana sinus merupakan kebalikan dari cosecan, cosinus kebalikan dari secan dan tangent kebalikan dari cotangent.
Sinus, Cosinus dan Tangent digunakan untuk menghitung sudut dengan perbandingan trigonometri sisi di segitiga.
Dengan gambar segitiga diatas, nilai Sinus, Cosinus dan Tangent diperoleh dengan cara sebagai berikut:
Sudut Istimewa
Berikut ini nilai sin, cos, dan tan untuk sudut istimewa:3
Dalam Kuadran
Sudut dalam suatu lingkaran, memiliki rentang 0° – 360°, sudut tersebut dibagi menjadi 4 kuadran, dengan masing-masing kuadran memiliki rentang sebesar 90°.- Kuadran 1 memiliki rentang sudut dari 0° – 90° dengan nilai sinus, cosinus dan tangent positif.
- Kuadran 2 memiliki rentang sudut dari 90° – 180° dengan nilai cosinus dan tangen negatif, sinus positif.
- Kuadran 3 memiliki rentang sudut dari 180° – 270° dengan nilai sinus dan cosinus negatif, tangen positif.
- Kuadran 4 memiliki rentang sudut dari 270° – 360° dengan nilai sinus dan tangent negatif, cosinus positif.
Perhatikan tabel trigonometri di bawah ini:
Identitas Trigonometri
Dalam suatu segitiga siku-siku, selalu berlaku prinsip phytagoras, yaitu  . Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
. Pada materi ini, prinsip phytagoras ini menjadi asal pembuktian identitas trigonometri sendiri.
Dari identitas yang pertama, dapat diperoleh bentuk lainnya, yaitu:
Bentuk ketiga yaitu  dibagi dengan
dibagi dengan 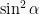 menjadi
menjadi 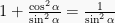 , dimana
, dimana  dan
dan  , sehingga diperoleh persamaan:
, sehingga diperoleh persamaan: 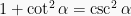 .
.
Contoh Soal Trignometri Kelas 10
Soal No. 1
Pada suatu lingkaran dibuat sebuah segi delapan beraturan seperti gambar
di bawah.
Jari-jari lingkaran
adalah 12 cm.
Tentukan:
a) panjang sisi segi-8
b) kelililing segi delapan tersebut!
Pembahasan
Segi delapan tersusun dari 8 buah segitiga sama kaki, dengan kedua kakinya
panjangnya 12 cm, sama dengan jari-jari lingkaran.
Ambil satu segitiga,
a) panjang sisi segi-8
Terapkan aturan kosinus
sebagai berikut:
b) Keliling segi delapan adalah 8 kali dari panjang sisinya
Soal No. 2
Dalam suatu lingkaran berjari-jari 8 cm, dibuat segi-8 beraturan. Tentukan
panjang sisi segi-8 tersebut!
Pembahasan
n = 8
r = 8 cm
Disini akan digunakan rumus jadi menentukan panjang sisi dari suatu segi-n
dalam lingkaran yang berjari-jari r
atau bentuk lain
dengan format kedua diperoleh
Soal No. 3
Nyatakan sudut-sudut berikut dalam satuan derajad:
a) 1/2 π rad
b) 3/4 π rad
c) 5/6 π rad
Pembahasan
Konversi:
1 π radian = 180°
Jadi:
a) 1/2 π rad
b) 3/4 π rad
c) 5/6 π rad
Soal No. 4
Nyatakan sudut-sudut berikut dalam satuan radian (rad):
a) 270°
b) 330°
Pembahasan
Konversi:
1 π radian = 180°
Jadi:
a) 270°
b) 330°
Soal No. 5
Diberikan sebuah segitiga siku-siku seperti gambar berikut ini.
Tentukan:
a) panjang AC
b) sin θ
c) cos θ
d) tan θ
e) cosec θ
f) sec θ
d) cotan θ
Pembahasan
a) panjang AC
Dengan phytagoras diperoleh panjang AC
b) sin θ
c) cos θ
d) tan θ
e) cosec θ
f) sec θ
g) cotan θ
Soal No. 6
Sebuah marka kejut dipasang melintang pada sebuah jalan dengan sudut 30° seperti ditunjukkan gambar berikut.
Jika panjang marka kejut adalah 8 meter, tentukan lebar jalan tersebut!
Pembahasan
Segitiga dengan sudut istimewa 30° dan sisi miring 8 m.
sin 30° = 1/2
sin 30° = BC/AC
BC/AC = 1/2
BC = 1/2 × AC = 1/2 × 8 = 4 meter
Lebar jalan = BC = 4 meter
Soal No. 7
Tentukan besar sudut C pada segitiga berikut!
Pembahasan
Data
AC = 5/3 √6 cm
BC = 5 cm
Dari data yang ada bisa ditentukan besar sudut B terlebih dahulu
Jumlah sudut segitiga adalah 180°sehingga besar sudut C adalah
∠C = 180 − (60 + 45) = 75°
Soal No. 8
Diberikan sebuah segitiga sama sisi ABC seperti gambar berikut. Panjang TC adalah 12 cm.
Tentukan panjang sisi segitiga tersebut!
Pembahasan
Δ ABC sama sisi, sehingga sudut A = sudut B = sudut C = 60° Jika diambil titik ATC menjadi segitiga, maka didapat gambar berikut.
Sinus 60° pada segitiga ATC adalah perbandingan sisi TC (sisi depan) dengan sisi AC (sisi miring) sehingga
Soal No. 8
Segitiga PQR dengan sisi-sisinya adalah p, q dan r. Jika p = 16 cm, r = 8√2 cm dan ∠ R = 30° tentukan besar ∠ P !
Pembahasan
Segitiga PQR
Berlaku aturan sinus
Besar sudut P dengan demikian adalah 45°
Soal No. 9
Diketahui segitiga ABC dengan panjang AC = AB = 6 cm. Sudut C sebesar 120°.
Tentukan luas segitiga ABC!
Soal No. 10
Segitiga samakaki ABC dengan sudut C = 30°.
Jika panjang BC = 12 cm, tentukan panjang AB!
Pembahasan
Dengan aturan kosinus
diperoleh
Soal No. 11
cos 315° adalah....
A. − 1/2 √3
B. − 1/2 √2
C. − 1/2
D. 1/2 √2
E. 1/2 √3
(Soal Ebtanas 1988)
Pembahasan
Sudut 315° berada di kuadran IV. Nilai-nilai cosinus sudut di kuadran IV memenuhi rumus berikut:
cos (360° − θ) = cos θ
Sehingga
cos 315° = (360° − 45°) = cos 45° = 1/2 √2
Soal No. 12
Diketahui:
PQ = 6 cm, QR = 9 cm dan ∠PQR = 120°
Tentukan kelililing segitiga PQR
Pembahasan
Mencari panjang PR
Keliling segitiga
= 6 cm + 9 cm + 3√19
= (15 + 3√19) cm
Soal No. 13
Seorang anak berdiri 20 meter dari sebuah menara seperti gambar berikut.
Perkirakan ketinggian menara dihitung dari titik A! Gunakan √2 = 1,4 dan √3 = 1,7 jika diperlukan.
Pembahasan
tan 60 ° adalah √3, asumsinya sudah dihafal. Sehingga dari pengertian tan sudut
Tinggi menara sekitar 34 meter.
Soal No. 14
Sebuah segitiga siku-siku.
Diketahui nilai dari sin β = 2/3. Tentukan nilai dari :
a) cos β
b) tan β
Pembahasan
sin β = 2/3 artinya perbandingan panjang sisi depan dengan sisi miringnya adalah 2 : 3
Gunakan phytagoras untuk menghitung panjang sisi yang ketiga (sisi samping):
Sehingga nilai cos β dan tan β berturut-turut adalah
Soal No. 15
Perhatikan gambar segitiga di bawah ini!
Tentukan perbandingan panjang sisi AB dan BC!
Pembahasan
Pada segitiga berlaku:
Sehingga perbandingan AB : BC = √2 : √3
sekian ya pembahasan tentang contoh soal trigonometri kelas 10. semoga dapat membantu

![Contoh Soal Trigonometeri Kelas 10 [+ Cara dan Pembahasan] Contoh Soal Trigonometeri Kelas 10 [+ Cara dan Pembahasan]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhDki89MH6ULBfYfMV0P2NH24voMjKXGkGGgxKt5eHeWrZoEbdy_ktVV68VjVtc-rfXzWKtHBKAvVaVnJJnXyuPQh2Xt_8Pi5RjBf9Lh2hnSHniMDuurzD18ZId65GCpc8ewHeJPCmQ5o4/d/trigonometri.png)



















































Kalo suka sama komputer. Cepet kawinin bang.. wkwkwk
ReplyDeleteN btw thanks soalnya😅✌
ahh, janganlah masih ada yang harus diperjuangin :v
DeleteTerimakasih soal nya kak
ReplyDelete