|
| Gelombang Longitudinal |
selamat ya sudah naik kelas. untuk materi pertama kelas 12 kali ini tentang gelombang bunyi. mari kita langsung saja kerjakan soalnya
Nomor 1
Diberikan sebuah persamaan gelombang Y = 0,02 sin (10πt − 2πx) dengan t dalam
sekon, Y dan x dalam meter.
Tentukan:
a. amplitudo gelombang
b. frekuensi sudut gelombang
c. tetapan gelombang
d. cepat rambat gelombang
e. frekuensi gelombang
f. periode gelombang
g. panjang gelombang
h. arah rambat gelombang
i. simpangan gelombang saat t = 1 sekon dan x = 1 m
j. persamaan kecepatan gelombang
k. kecepatan maksimum gelombang
l. persamaan percepatan gelombang
m. nilai mutlak percepatan maksimum
n. sudut fase saat t = 0,1 sekon pada x = 1/3 m
o. fase saat t = 0,1 sekon pada x = 1/3 m
Pembahasan :
Bentuk persamaan umum
gelombang:
Y = A sin (ωt - kx)
dengan A amplitudo
gelombang, ω = 2πf dan k = 2π/λ dengan demikian :
a. A = 0,02 m
b. ω = 10π rad/s
c. k = 2π
d. v = ω/k = 10π/2π = 5 m/s
e. f = ω/2π = 10π/2π =
5 Hz
f. T = 1/f = 1/ 5 = 0,
2 sekon
g. λ = 2π/k = 2π/2π =
1 m
h. ke arah sumbu x positif
i. Y = 0,02 sin(10 π-
2π) = 0,02 sin(8π) = 0 m
j. v = ω A cos(ωt−kx) = 10π(0,02) cos(10πt−2πx) m/s
k. vmaks = ωA = 10π(0,02) m/s
l. a = −ω2y = −(10π)2 (0,02) sin(10πt
− 2πx) m/s2
m. amaks = |−ω2A| = |−(10π)2 (0,02)| m/s2
n. sudut fase θ = (10.π.0,1−2π.(1/3) = 1/3 π = 60o
o. fase φ = 60o/360o = 1/6
Nomor 2
Suatu gelombang permukaan air yang frekuensinya 500 Hz merambat dengan
kecepatan 350 m/s. tentukan jarak antara dua titik yang berbeda sudut fase
60°!
(Sumber : Soal SPMB)
Pembahasan :
Lebih dahulu tentukan
besarnya panjang gelombang dimana
Beda fase gelombang antara dua titik yang jaraknya diketahui adalah
Nomor 3
Seutas tali salah satu ujungnya digerakkan naik turun sedangkan ujung lainnya
terikat. Persamaan gelombang tali adalah y = 8 sin (0,1π) x cos π (100t - 12)
dengan y dan x dalam cm dan t dalam satuan sekon. Tentukan:
a. panjang gelombang
b. frekuensi gelombang
c. panjang tali
(Sumber : Soal Ebtanas)
Pembahasan :
Pola dari gelombang
stasioner diatas adalah
a. menentukan panjang gelombang
b. menentukan frekuensi gelombang
c. menentukan panjang tali
Nomor 4
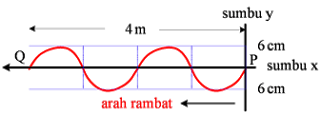
Diberikan grafik dari suatu gelombang berjalan seperti gambar di bawah!
Jika jarak P ke Q
ditempuh dalam waktu 5 sekon, tentukan persamaan dari gelombang di atas!
(Tipikal Soal UN)
Pembahasan :
Bentuk umum persamaan
gelombang adalah
atau
atau
dengan perjanjian tanda sebagai berikut :
Tanda Amplitudo (+)
jika gerakan pertama ke arah atas
Tanda Amplitudo (-)
jika gerakan pertama ke arah bawah
Tanda dalam kurung (+)
jika gelombang merambat ke arah sumbu X negatif / ke kiri
Tanda dalam kurung (-)
jika gelombang merambat ke arah sumbu X positif / ke kanan
ambil data dari soal
panjang gelombang (λ) = 2 meter, dan periode (T) = 5/2 sekon atau frekuensi (f)
= 2/5 Hz, masukkan data ke pola misal pola ke 2 yang dipakai didapat
Nomor 5
Seutas kawat bergetar menurut persamaan :
Jarak perut ketiga
dari titik x = 0 adalah.....
A. 10 cm
B. 7,5 cm
C. 6,0 cm
D. 5,0 cm
E. 2,5 cm
Sumber Soal : Marthen Kanginan 3A Gejala Gelombang
Pembahasan :
Pola diatas adalah
pola untuk persamaan gelombang stasioner ujung tetap atau ujung terikat. Untuk
mencari jarak perut atau simpul dari ujung ikatnya, tentukan dulu nilai dari
panjang gelombang.
Setelah ketemu panjang gelombang, tinggal masukkan rumus untuk mencari perut ke
-3 . Lupa rumusnya,..!?! Atau takut kebalik-balik dengan ujung bebas,..!? Ya
sudah tak usah pakai rumus, kita pakai gambar saja seperti di bawah:
Posisi perut ketiga P3 dari ujung tetap A adalah satu seperempat panjang gelombang atau
(5/4) λ (Satu gelombang =
satu bukit - satu lembah), sehingga nilai X adalah :
X = (5/4) λ = (5/4) x
6 cm = 7,5 cm
Nomor 6
Sebuah gelombang transversal memiliki frekuensi sebesar 0,25 Hz. Jika jarak
antara dua buah titik yang berurutan pada gelombang
yang memiliki fase sama adalah 0,125 m, tentukan cepat
rambat gelombang tersebut, nyatakan dalam satuan cm/s!
Pembahasan
Data dari soal:
f = 0,25 Hz
Jarak dua titik yang berurutan dan sefase:
λ = 0, 125 m
ν = .....
ν = λ f
ν = (0,125)(0,25) = 0,03125 m/s = 3,125 cm/s
Nomor 7
Sebuah gelombang transversal memiliki frekuensi sebesar 0,25 Hz. Jika jarak
antara dua buah titik yang berurutan pada gelombang
yang memiliki fase berlawanan adalah 0,125 m, tentukan
cepat rambat gelombang tersebut, nyatakan dalam satuan cm/s!
Pembahasan
Data dari soal:
f = 0,25 Hz
Jarak dua titik yang berurutan dan berlawanan fase:
1/2λ = 0, 125 m → λ = 2 ×
0,125 = 0,25 m
ν = .....
ν = λ f
ν = (0,25)(0,25) = 0,0625 m/s = 6,25 cm/s
Nomor 8
Diberikan sebuah persamaan gelombang:
y = 0,05 cos (10t + 2x) meter
Tentukan :
a) Persamaan kecepatan
b) Persamaan percepatan
Pembahasan
( y)
↓ diturunkan
( ν)
↓ diturunkan
( a)
y = 0,05 cos (10t + 2x) meter
Jika y diturunkan,
akan diperoleh v :
ν = − (10)(0,05) sin (10t + 2x)
ν = − 0,5 sin (10t + 2x) m/s
Jika v diturunkan,
akan diperoleh a :
a = − (10)(0,5) cos (10t + 2x)
a = − 5 cos (10t + 2x) m/s2