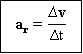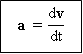Rangkuman Materi Kinematika dengan Analisis Vektor
Selamat ya buat temen-temen yang udah naik ke kelas 11. semakin tinggi tingkatan kelas, maka makin sulit juga matapelajaran yang akan dihadapi.
materi awal fisika kelas xi yaitu tentang kinematika dengan analisis vektor. beberapa materi yang dibahas disini adalah contoh soal gerak parabola dan juga gerak melingkar yang disertai dengan pembahasan.
penyelesaian yang runtut akan membantu teman-teman dalam memahami materinya. jangan lupa juga untuk mendownload rangkuman rumus kinematika gerak yang berbentuk pdf pada link dibawah ya. selamat belajar
Saran Artikel : Pembahasan fisika erlangga kinematika dengan analisis vektor
Vektor satuan.
• Vektor yang mengarah sumbu x satuannya i.
• Vektor yang mengarah sumbu y satuannya j.
• Vektor yang mengarah sumbu z satuannya k.
Vektor posisi
Dengan r adalah vektor posisi, x menyatakan titik koordinat pada sumbu x dan y adalah titik koordinat pada sumbu y.
Vektor perpindahan
Perpindahan adalah perubahan posisi suatu partikel dalam selang waktu tertentu.
Dengan Δr menyatakan vektor perpindahan dan r1 dan r2 menyatakan vektor posisi pertama dan kedua.
Vektor kecepatan rata-rata
Adalah hasil bagi antara vektor perpindahan (Δr) dengan selang waktu (Δt).
Dengan vr = vektor kecepatan rata-rata.
Vektor kecepatan sesaat
Adalah turunan pertama dari fungsi posisi (r) terhadap waktu (t).
Vektor percepatan rata-rata
Adalah perubahan kecepatan (Δv) dalam selang waktu (Δt) tertentu.
Vektor percepatan sesaat
Adalah turunan pertama dari fungsi kecepatan (v) terhadap waktu (t).
Menentukan vektor posisi dari vektor kecepatan
Menentukan vektor kecepatan dari vektor percepatan
GERAK MELINGKAR
Posisi sudut (θ) dan perpindahan sudut (Δθ)
Dengan Δθ menyatakan perpindahan sudut, θ1 dan θ2 menyatakan posisi sudut pertama dan kedua.
Kecepatan sudut rata-rata
Adalah hasil bagi antara perpindahan sudut (Δθ) dengan selang waktu (Δt).
Kecepatan sudut sesaat
Adalah turunan pertama dari fungsi posisi sudut (θ) terhadap waktu (t).
Vektor percepatan sudut rata-rata
Adalah perubahan kecepatan sudut (Δω) dalam selang waktu (Δt) tertentu.
Vektor percepatan sudut sesaat
Adalah turunan pertama dari fungsi kecepatan sudut (ω) terhadap waktu (t).
Menentukan posisi sudut dari kecepatan sudut
Menentukan kecepatan sudut dari percepatan sudut
GERAK PARABOLA
Waktu untuk mencapai ketinggian maksimum
Ketinggain maksimum
Jangkauan maksimum/jarak mendatar.
Keterangan:
t = waktu mencapai ketinggian maksimum (s).
v0 = kecepatan awal (m/s).
θ = sudut elevasi.
g = percepatan gravitasi (10 m/s2).
h = ketinggian maksimum.
x = jangkauan/jarak mendatar (m).
Soal dan Pembahasan Kinematika dengna Analisis Vektor
Nomor 1
Jika sebuah pertikel bergerak dengan persamaan posisi r = 5t2 +
1, kecepatan rata-rata antara t1 = 2 s dan t2 = 3 s adalah...
A. 25 m/s
B. 30 m/s
C. 35 m/s
D. 40 m/s
E. 45 m/s
Pembahasan:
a. Terlebih dahulu hitung r1 → t1 = 2 s
r1 =
5t2 + 1 = 5 (2)2 + 1 = 5 . 4 + 1
r1 =
21 m
b. Menghitung r2 →
t2 =
3 s
r1 =
5t2 + 1 = 5 (3)2 + 1 = 5 . 9 + 1
r1 =
46 m
c. Menghitung perpindahan Δr.
Δr = r2 –
r1 =
46 – 21 = 25 m
d. Menghitung kecepatan rata-rata vr.
Nomor 2
Sebuah partikel pada t1 =
0 berada pada koordinat (2,4) dan t2 = 2 detik berada pada (8,6) maka vektor kecepatan
rata-ratanya adalah...
A. 3 i + 2 j
B. 4 i + 3j
C. 3i + j
D. 2i + 4 j
E. 4i + 3j
Pembahasan:
a. Terlebih dahulu tentukan persamaan posisi r1 (2,4).
r1 = x i + y j = 2 i + 4 j
Ingat!
(2,4) berarti x = 2 dan y = 4.
b. Persamaan posisi r2 (8,6).
r2 =
x i + y j = 8 i + 6 j
c. Persamaan perpindahan Δr
Δr = r2 –
r1 =
(8 i + 6 j) – (2 i + 4 j)
Δr = 8 i + 6 j – 2 i – 4 j = 6 i + 2 j
Ingat!
Vektor dapat dijumlahkan jika vektor satuannya sama.
d. Persamaan vektor kecepatan vr.
Saran Artikel : Pembahasan kimia erlangga kelas 11